Alex Sikorski

Jun 23, 2022

Maximum 69 Number (LeetCode #1323)

The problem starts by explaining what num is:

You are given a positive integer num consisting only of digits 6 and 9.

Return the maximum number you can get by changing at most one digit (6 becomes 9, and 9 becomes 6).

Example 1:

Input: num = 9669
Output: 9969
Explanation: 
Changing the first digit results in 6669.
Changing the second digit results in 9969.
Changing the third digit results in 9699.
Changing the fourth digit results in 9666.
The maximum number is 9969.

Example 2:

Input: num = 9996
Output: 9999
Explanation: Changing the last digit 6 to 9 results in the maximum number.

Example 3:

Input: num = 9999
Output: 9999
Explanation: It is better not to apply any change.

Constraints:

1. 1 <= num <= 104
2. num consists of only 6 and 9 digits.

Initial Thoughts

It's clear to me that we will have to seek out the first 6 within the int num, left to right. The reason for this is that the digits positioned most left, if changed, will lead to a larger maximum number.

Logically speaking, we would never want to switch a 9 to a 6 since that would only ever lead to a smaller number.

So once we find the first 6 in our number, what do we do? Well, since we know we will only ever switch from a 6 to a 9, and the difference between those two numbers is 3, we can calculate a new maximum.

I created the following formula to help understand on getting the max value based on the information above: ⁠Maximum number = num + (3 * (10^(L - 1 - i)))

Let's say the num = 9969, and num is a String. ⁠Length = L = num.length(); = 4. ⁠We know that the 6 is placed on index i = 2, so i = 2.

Maximum number = 9969 + (3 * (10^(4 - 1 - 2))) = 9999

We are essentially adding 3*1 or 3*10 or 3*100 or 3*1000 depending on the position of the most left 6 found in num.

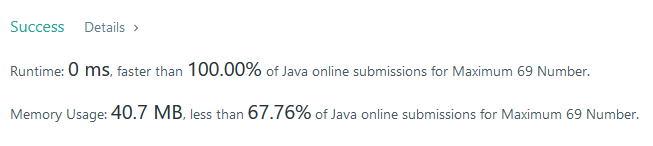
Solution

class Solution {
    public int maximum69Number (int num) {
        String s = String.valueOf(num);
        for(int i = 0; i < s.length(); i++)
            if(s.charAt(i) == '6') return (int) (num + ((Math.pow(10, s.length() - 1 - i)) * 3));
        return num;
    }
} 

Result